Sub Chapter 7.3
7.3 Arithmetic Circuits - Basic Building Blocks
1. Tujuan [kembali]
Mempelajari tentang bagaimana materi aritmatika rangkaian
Mampu mengaplikasikan aritmatika rangkaian
Mampu membuat rangkaian aritmatika rangkaian
2. Alat dan Bahan [kembali]
3. Dasar Teori [kembali]
7.3.1 half adder
Half adder adalah sebuah sirkuit aritmatika yang biasa digunakan untuk menjumlahkan 2 buah bit. Half adder memiliki 2 buah input yang merepresentasikan 2 bit dan 2 buah output dengan yang satu memproduksi SUM dan yang lain memproduksi CARRY
Gambar 7.4 Tabel kebenaran dari half adder
Implementasi logika dari half adder
7.3.2 full adder
Sedangkan full adder memiliki 3 input untuk memproduksi SUM dan CARRY
Tabel kebenaran dari full adder
Aljabar boolean dari full adder
Sirkuit logika dari full adder
7.3.3 half subtractor
Half subtractor adalah sebuah kombinasi sirkuit yang biasa digunakan untuk mengurangkan 1 digit binary dengan 1 digit yang lainnya untuk memproduksi DIFFERENCE output dan sebuah BORROW output
Aljabar boolean half subtractor
Tabel kebenaran dari half subtractor
Diagram logika half subtractor
7.3.4 full subtractor
Dibanding half subtractor, full subtractor memiliki 3 input.
Aljabar boolean dari full subtractor
Tabel kebenaran dari full subtractor
Implementasi logika dari full subtractor dengan half subtractor
7.3.5 controlled inverter
Controlled inverter biasa digunakan untuk menemukan first complement.
a) Controlled inverter 1 bit b) controlled inverter 8 bit
Sebagai contoh, jika diketahui input 11010010 akan memproduksi 00101101 pada outputnya.
4. Percobaan [kembali]
A. Prosedur Percobaan
Buka poteus
- Buka sinematic captures
- Buka library dan pilih komponen yang sesuai
- Pilih terminal yang di perlukan
- Rangkai komponen sehingga membentuk rangkaian
- Tangbahkan Voltmeter untuk mengukur tegangan poda resistor dan transistor
- Klik tombol Play dan jalankan simulasinya
B. Rangkaian Simulasi
Gambar Rangkaian
Rangkaian 7.5A (bit biner pertama), (bit biner kedua), dan (carry-in dari penjumlahan sebelumnya). Rangkaian ini menggunakan dua gerbang logika XOR untuk menghasilkan output Sum (S). Pertama, input dan dimasukkan ke gerbang XOR, yang menghasilkan . Hasil dari gerbang XOR pertama ini kemudian dikombinasikan dengan menggunakan gerbang XOR kedua, menghasilkan . Input dari A⊕B akan dikalikan dengan Cin lalu output tersebut akan ditambahkan dengan A*B sehingga output dari (A⊕B)*Cin +A*B disebut bitCarry
Ketika kedua input dan dimasukkan ke dalam gerbang XOR, keluaran gerbang ini adalah bit Sum. Input dan juga dimasukkan ke dalam gerbang AND, dan keluaran gerbang ini adalah bit Carry
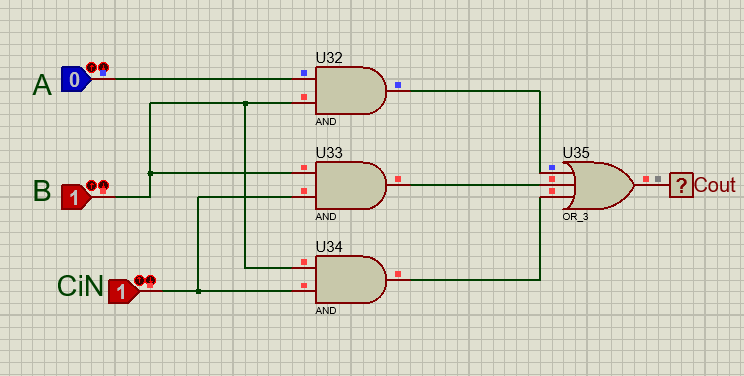
Rangkaian ini merupakan summing dari bit A,B, dan Cin yang di kalikan. Inputan ke logika OR terdiri dari 4 logika AND yang mana divariasikan untuk bit A, B dan Cin.
Rangkaian 7.9 b
Rangkaian ini merupakan summing dari bit A,B, dan Cin yang di kalikan. Inputan ke logika OR terdiri dari 3 logika AND yang mana divariasikan untuk bit A, B dan Cin.
Rangkaian 7.6Rangkaian 7.11 a
Rangkaian Full Adder menggunakan Rangkaian Dalam
Ketika kita ingin menambahkan 2 bit atau lebih maka kita memerlukan 2 atau lebih rangkaian full adder sehingga untuk mensederhanakan rangkaian kita membuat IC dengan rangkaian didalamnya adalah rangkaian full addermelakukan operasi pengurangan pada dua bit biner dengan dua input, yaitu bit minuend () dan bit subtrahend (). Rangkaian ini memiliki dua output: Difference (selisih) dan Borrow (pinjaman). Output Difference dihitung menggunakan gerbang logika XOR, di mana , yang memberikan keluaran 1 jika hanya salah satu dari input atau B yang bernilai 1. Output Borrow dihitung menggunakan kombinasi gerbang logika NOT dan AND, di mana, yang memberikan keluaran 1 jika A= 0 dan = 1, menunjukkan bahwa diperlukan pinjaman. Dalam rangkaian ini, gerbang NOT membalik nilai sebelum digunakan bersama dalam gerbang AND. Dengan demikian, half subtractor secara efektif menghitung selisih dan menentukan apakah ada kebutuhan untuk pinjaman dalam proses pengurangan dua bit biner
Rangkaian Half Substactor menggunakan Rangkaian Dalam
Ketika kita ingin mengurangkan 2 bit atau lebih maka kita memerlukan 2 atau lebih rangkaian full adder sehingga untuk mensederhanakan rangkaian kita membuat IC dengan rangkaian didalamnya adalah rangkaian Half Substactor
Rangkaian Full Substactor
melakukan operasi pengurangan pada dua bit biner dengan mempertimbangkan bit pinjaman dari operasi sebelumnya. Rangkaian ini memiliki tiga input: minuend (), subtrahend (), dan borrow-in (). Output dari rangkaian ini terdiri dari Difference (selisih) dan Borrow-out (pinjaman). Output Difference dihitung menggunakan kombinasi dua gerbang XOR, yaitu , yang memberikan hasil 1 jika jumlah bit yang bernilai 1 adalah ganjil. Untuk menghitung Borrow-out, kombinasi gerbang AND dan OR digunakan:
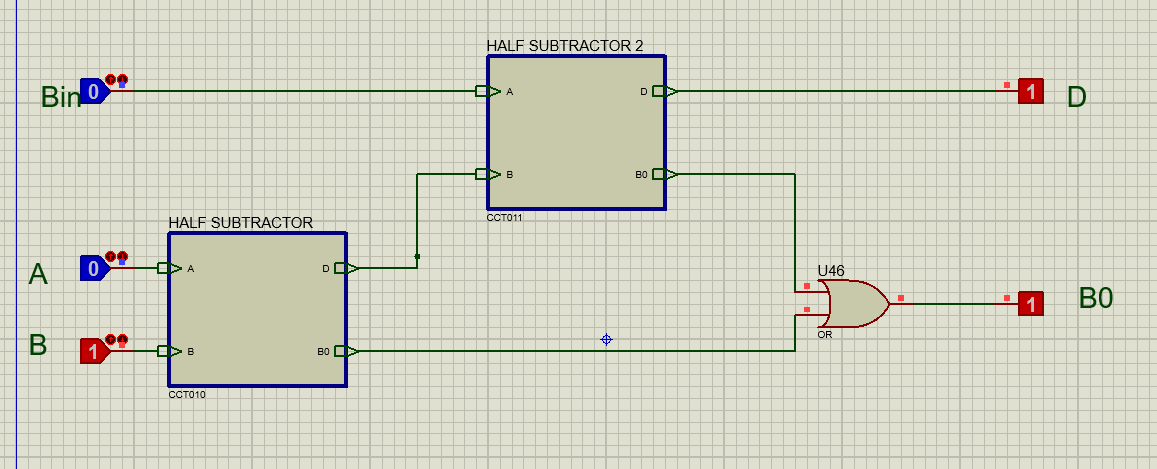
Rangkaian Full Substactor menggunakan Rangkaian Dalam
Rangkaian full substractor terdiri dari 2 half substractor, kita membuat 2 buah IC yang terdiri dari half substractor yang mana output D1 dari IC pertama menjadi input B2 dari IC kedua sehingga nilai dari D1*Bin adalah output D dan nilai B01 + B01 = B0
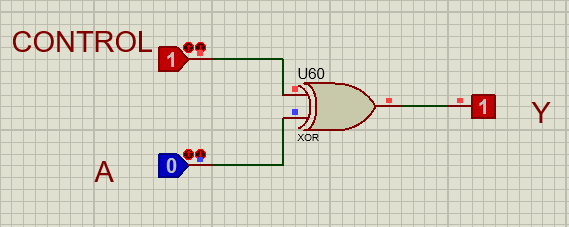
Rangkaian Controlled inverter
Rangkaian Controlled inverter
melibatkan penggunaan sebuah sinyal kontrol untuk menentukan apakah input biner akan di-inversi (dibalik) atau diteruskan tanpa perubahan ke output. Rangkaian ini memiliki dua input: satu input utama () dan satu sinyal kontrol (). Output dari rangkaian ini adalah . Jika sinyal kontrol () bernilai 0, output () akan sama dengan input (), artinya input diteruskan langsung ke output tanpa perubahan. Namun, jika sinyal kontrol () bernilai 1, output () akan menjadi inversi dari input (), yaitu . Secara teknis, ini bisa dicapai dengan menggunakan gerbang XOR, di mana output adalah hasil dari operasi . Ketika bernilai 0, , dan ketika bernilai 1,‾ Y = A \oplus 1 = \overline{A}
5. Video [kembali]
6. Example [kembali]
1) Untuk rangkaian half adder pada Gambar (a), input yang diterapkan pada A dan B seperti ditunjukkan pada Gambar (b). Plot output SUM dan CARRY yang sesuai pada skala yang sama!
Jawaban: Bentuk gelombang SUM dan CARRY dapat diplot dari pengetahuan kita tentang tabel kebenaran half adder. Yang perlu kita ingat untuk menyelesaikan masalah ini adalah 0+0 menghasilkan '0' sebagai keluaran SUM dan '0' sebagai CARRY. 0+1 atau 1+0 menghasilkan '1' sebagai keluaran SUM dan '0' sebagai CARRY. 1+1 menghasilkan '0' sebagai output SUM dan '1' sebagai CARRY. Bentuk gelombang keluaran seperti yang ditunjukkan pada Gambar dibawah:
2) Mengingat ekspresi Boolean yang relevan untuk rangkaian half adder dan half subtractor, rancanglah rangkaian half adder subtractor yang dapat digunakan untuk melakukan penjumlahan atau pengurangan pada dua bilangan satu bit. Operasi aritmatika yang diinginkan harus dapat dipilih dari input control!
Jawaban:
Ekspresi Boolean untuk half adder dan half subtractor diberikan sebagai berikut:
Half adder:
Half subtractor:
Jika kita menggunakan inverter terkontrol untuk melengkapi A dalam kasus rangkaian half subtractor, maka perangkat keras yang sama juga dapat digunakan untuk menjumlahkan dua bilangan satu bit.
Gambar di atas menunjukkan diagram rangkaian logika. Ketika input kontrol adalah '0', variabel input A dilewatkan tanpa pelengkap ke input gerbang NAND. Dalam hal ini, gerbang AND menghasilkan keluaran CARRY dari operasi penjumlahan. Gerbang EX-OR menghasilkan keluaran SUM. Di sisi lain, ketika input kontrol adalah '1', gerbang AND menghasilkan output BORROW dan gerbang EX-OR menghasilkan output DIFFERENCE. Jadi, '0' pada masukan kontrol menjadikannya setengah penambah, sedangkan '1' pada masukan kontrol menjadikannya setengah pengurang.
7. Problem [kembali]
1) Sebuah komputer menerima dua bilangan biner sebagai input, yaitu A = 1011 dan B = 1101. Tentukan outputnya menggunakan rangkaian half adder!
Jawaban:
Output dari Half Adder adalah S = 0 dan Cout = 1.
Dalam bilangan biner, A = 1011 dan B = 1101. Ketika dijumlahkan menggunakan Half Adder, jumlahnya adalah S = 0 dan carry-out adalah Cout = 1. Hal ini terjadi karena bit pertama dari A dan B bertemu dengan kondisi 1 + 1 yang menghasilkan 0 dengan carry-out 1.
2) Sebuah Full Adder menerima tiga bit input, yaitu A = 011, B = 101, dan carry-in Cin = 1. Hitunglah outputnya!
Jawaban:
Output dari Full Adder adalah S = 1 dan Cout = 1.
Dengan bit input A = 011, B = 101, dan carry-in Cin = 1, Full Adder menghasilkan output S = 1 dan carry-out Cout = 1. Hal ini terjadi karena penjumlahan bit terakhir menghasilkan 1 + 1 + 1, yang menghasilkan 1 dengan carry-out 1.
3) Jelaskan prinsip kerja dari rangkaian Full Adder dan berikan contoh penggunaannya dalam penjumlahan biner yang kompleks!
Jawaban:
Rangkaian Full Adder adalah rangkaian aritmetika digital yang menerima tiga input, yaitu dua bit yang akan dijumlahkan (A dan B) serta carry-in (Cin) dari penjumlahan sebelumnya. Prinsip kerjanya mirip dengan Half Adder, namun Full Adder juga memperhitungkan carry-in dari bit sebelumnya. Outputnya terdiri dari dua bagian, yaitu jumlah (sum) dan carry-out (Cout).
Dalam penjumlahan biner yang kompleks, seperti saat menambahkan dua bilangan biner dengan banyak bit, rangkaian Full Adder digunakan. Setiap rangkaian Full Adder akan menerima dua bit dari bilangan yang akan dijumlahkan dan carry-in dari penjumlahan sebelumnya. Contohnya, saat menambahkan bilangan biner yang memiliki lebih dari satu digit seperti 1101 + 1010. Dalam hal ini, rangkaian Full Adder digunakan untuk menangani setiap pasangan bit.
8. Pilihan Ganda [kembali]
1) Apa yang dilakukan oleh rangkaian Half Adder?
a. Menambahkan dua bilangan biner
b. Mengurangi dua bilangan biner
c. Mengalikan dua bilangan biner
d. Membandingkan dua bilangan biner
Jawab: Half Adder adalah rangkaian sederhana yang digunakan untuk menambahkan dua bit tunggal. Ini memiliki dua input, yaitu bit pertama (A) dan bit kedua (B), dan menghasilkan dua output, yaitu jumlah (sum) dan carry-out. Half Adder hanya dapat menangani penjumlahan dua bit tunggal tanpa mempertimbangkan carry-in dari bit sebelumnya.
2) Berapa banyak input yang digunakan oleh Full Adder?
a. 1
b. 2
c. 3
d. 4
Jawab: Full Adder adalah rangkaian yang digunakan untuk menambahkan tiga bit, yaitu dua bit input dan carry-in dari bit sebelumnya. Dengan demikian, Full Adder memiliki tiga input: dua bit pertama yang akan dijumlahkan (A dan B) dan carry-in dari bit sebelumnya (Cin).
3) Apa perbedaan antara Half Adder dan Full Adder?
a. Half Adder hanya dapat menambahkan dua bit, sementara Full Adder dapat menambahkan tiga bit.
b. Half Adder menggunakan dua input, sementara Full Adder menggunakan tiga input.
c. Half Adder menghasilkan carry-out, sementara Full Adder menghasilkan carry-in.
d. Half Adder hanya dapat melakukan operasi penjumlahan, sementara Full Adder dapat melakukan operasi penjumlahan dan pengurangan.
Jawab: Half Adder memiliki dua input (A dan B) untuk menambahkan dua bit tunggal, sedangkan Full Adder memiliki tiga input (A, B, dan Cin) untuk menambahkan tiga bit, termasuk carry-in dari bit sebelumnya. Dengan demikian, Full Adder lebih kompleks daripada Half Adder karena dapat menangani penjumlahan lebih banyak bit.
9. Download File[kembali]
Download File html (download)
Download Rangkaian Half Adder (download)
Download Rangkaian Full Adder Dengan Output bitSum (download)
Download Rangkaian Full Adder Dengan Output bitCarry (download)
Download Rangkaian Full Adder (download)
Download Rangkaian Full Adder dengan Rangkaian Dalam (download)
Download Rangkaian Half Substractor (download)
Download Rangkaian Half Substractor menggunakan Rangkaian Dalam (download)
Download Rangkaian Full Substractor (download)
Download Rangkaian Full Substractor menggunakan Rangkaian Dalam (download)
Download Rangkaian Controlled Inverter (download)
Download Rangkaian Controlled Inverter 2 (download)





































Komentar
Posting Komentar